Γιατί πλέει ένα σκάφος; – Η Αρχή του Αρχιμήδη και η εφαρμογή της στη ναυπηγική
Τα σκάφη και τα μυστικά τουςΗ Αρχή του Αρχιμήδη και η εφαρμογή της στη ναυπηγική
Του Μάκη Ματιάτου
Όλα ξεκίνησαν από τον Αρχιμήδη και το περίφημο «εύρηκα-εύρηκα». Είναι η αρχή της υδροστατικής και ειδικότερα η μελέτη της συμπεριφοράς των αντικειμένων, που πλέουν ή είναι βυθισμένο στο νερό. Ο Αρχιμήδης ανακάλυψε και κατέγραψε πολλούς νόμους της υδροστατικής, με φυσικά τον πιο γνωστό μας σαν «Αρχή του Αρχιμήδη».

Με απλά λόγια ο Αρχιμήδης βρήκε πως όταν ένα στερεό σώμα βυθίζεται στο νερό, εκτοπίζει μια μάζα νερού, το βάρος της οποίας είναι ίσο με αυτό του σώματος που βυθίζεται. Επίσης, όταν ένα σώμα είναι μερικώς ή ολικώς βυθισμένο στο νερό, υφίσταται μια προς τα πάνω δύναμη πλευστότητας που είναι ίση με το βάρος του νερού που εκτοπίζεται.
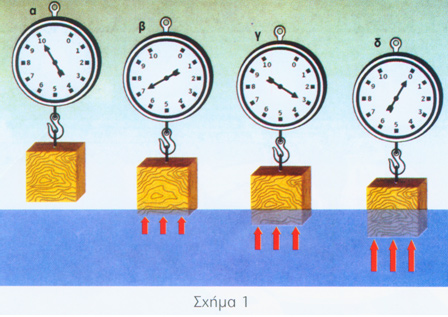
Στην περίπτωση του σκάφους τώρα, όταν αυτό πλέει στο νερό εκτοπίζει κάποια ποσότητα νερού, για να δημιουργήσει μια «τρύπα» σαν καλούπι, που παίρνει το σχήμα των υφάλων του. Ο όγκος αυτός της τρύπας ή του καλουπιού είναι απλά ο όγκος του νερού που εκτοπίστηκε. Το σχήμα 1 είναι ένα χαρακτηριστικό παράδειγμα της Αρχής του Αρχιμήδη. Πρόκειται για ένα κομμάτι ξύλο που κρέμεται από μια ζυγαριά. Όπως ξέρουμε, το ξύλο επιπλέει (βυθίζεται μερικώς). Το βάρος του ξύλου, όπως φαίνεται στην περίπτωση α είναι 10 κιλά (έξω από το νερό). Καθώς βυθίζουμε το ξύλο στο νερό (σχήμα 1 β και 1γ) παρατηρούμε πως χάνει από το βάρος του τόσο όσο είναι η προς τα πάνω δύναμη πλευστότητας, δηλαδή η άντωση. Στην περίπτωση 1β έχει χάσει τρία κιλά, ενώ εξασκείται πάνω του μια δύναμη άντωσης τριών κιλών. Αντίστοιχα, στο σχήμα 1γ, έχει χάσει επτά κιλά και η δύναμη άντωσης έχει φτάσει την τιμή των επτά κιλών. Στην περίπτωση 1δ, το κομμάτι του ξύλου πλέει στο νερό, έχει χάσει το βάρος του και έχει δημιουργήσει μια δύναμη άντωσης ίση με το βάρος που είχε αρχικά πριν μπει στο νερό.
Η ίδια αρχή που ισχύει για τα σώματα που πλέουν, ισχύει και γιΆ αυτά που βυθίζονται, μόνο που τώρα υπεισέρχεται άλλα μια έννοια, αυτή της πυκνότητας. Πυκνότητα ή ειδικό βάρος ενός σώματος είναι το βάρος του σώματος δια του όγκου (μάζα) του:
Πυκνότητα ή ειδικό βάρος = Βάρος / Όγκος (ε = Β/Ο).
Από τον παραπάνω ορισμό προκύπτουν οι σχέσεις:
Βάρος (Β) = Όγκος (Ο) x ειδικό βάρος (ε)
Όγκος (O) = Βάρος (Β) / ειδικό βάρος (ε)
Για να βρούμε την πυκνότητα ενός στερεού σώματος, πρώτα το ζυγίζουμε στον αέρα και στη συνέχεια το βυθίζουμε στο (αποσταγμένο) νερό. Έστω ότι ζυγίζοντας κάποιο σώμα στον αέρα βρίσκουμε ότι είναι 665 γραμμάρια και στο νερό 580 γραμμάρια. Κατά τον Αρχιμήδη, η διαφορά του βάρους, δηλαδή 665 – 580 = 85 γραμμάρια, είναι το βάρος του νερού που εκτοπίστηκε, δηλαδή το βάρος του όγκου του εκτοπισμένου νερού που είναι ίσο με τον όγκο του σώματος. Το ειδικό βάρος ή πυκνότητα του σώματος είναι
ε = 665 / 85 = 7,8 γραμμάρια ανά κυβικό εκατοστό (gr/cm³) ή 7,8 κιλά ανά κυβικό μέτρο (kg/m³).
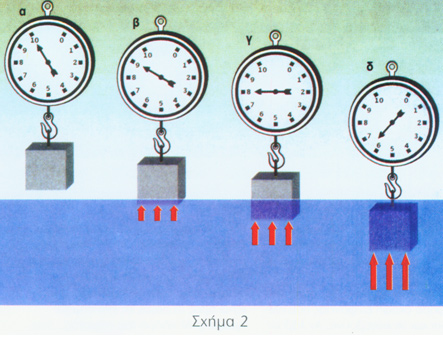
Ας δούμε στο σχήμα 2 ένα ακόμα παράδειγμα με τη ζυγαριά, αυτή τη φορά όμως λαμβάνοντας υπόψη μας και την έννοια της πυκνότητας. Το σώμα που θα βυθίσουμε τώρα είναι ένας γρανίτης βάρους 10 κιλών και φυσικά ξέρουμε πως βυθίζεται τελείως, επειδή ο γρανίτης έχει μεγαλύτερη πυκνότητα από το ξύλο, 2,7 kg/m³ και 0,45 kg/m³ αντίστοιχα, δηλαδή έχει το 1/6 περίπου του όγκου του ξύλου και υφίσταται το 1/6 της δύναμης άντωσης. Όταν ο γρανίτης βυθισθεί τελείως, ο μικρότερος όγκος του «παράγει» μόνο 3,6 κιλά άντωσης (1/6 του βάρους) και το βάρος του φτάνει τα 6,4 κιλά.
Κάνοντας το ίδιο παράδειγμα στο σχήμα 3, τη φορά αυτό με ένα κομμάτι μολύβι 10 κιλών, που έχει πυκνότητα 11,3 kg/m³, δηλαδή έχει όγκο περίπου το 1/25 του αντίστοιχου γρανίτη, βλέπουμε πως υφίσταται μόλις 0,9 κιλά άντωσης (1/25 του βάρους), ενώ το βάρος του φτάνει τα 9,1 κιλά όταν βυθισθεί τελείως στο νερό.
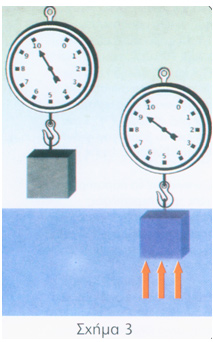
Γενικά, μπορούμε να παρατηρήσουμε τις εξής τρεις περιπτώσεις:
1. Όταν το βάρος του σώματος είναι μεγαλύτερο από το βάρος του υγρού που εκτοπίζεται, το σώμα βυθίζεται στον πυθμένα.
2. Όταν το βάρος του σώματος είναι ίσο με το βάρος του εκτοπιζομένου υγρού, το σώμα ούτε βυθίζεται, ούτε ανέρχεται, αλλά ισορροπεί μετέωρο στο υγρό.
3. Όταν το σώμα έχει βάρος μικρότερο από αυτό του εκτοπιζομένου
υγρού, ανέρχεται μέχρι την επιφάνεια και πλέει, δηλαδή μέρος του σώματος βρίσκεται πάνω από την επιφάνεια τόσο, όσο το βυθισμένο μέρος του να εκτοπίζει κάποιον όγκο υγρού ίσο με το βάρος του σώματος.
Χαρακτηριστικό παράδειγμα, πέρα από τα διάφορα σκάφη επιφανείας που πλέουν, είναι και τα παγόβουνα. Αν λάβουμε υπόψη μας τη μικρή διαφορά
βάρους μεταξύ του θαλασσινού νερού και ίσου όγκου πάγου (1,027- 0,918 = 0,109), βλέπουμε γιατί το τμήμα του πάγου κάτω από την επιφάνεια του νερού είναι 8-9 φορές μεγαλύτερο αυτού που εξέχει στην επιφάνεια.
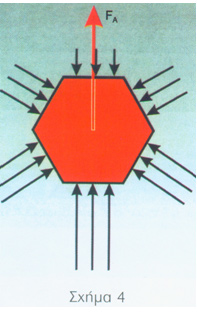
Στο σημείο αυτό θα πρέπει να δούμε τι είναι η άντωση. Στο σχήμα 4 βλέπουμε ένα σώμα με ένα όγκο V βυθισμένο στο νερό. Σε κάθε στοιχειώδη επιφάνεια του σώματος ασκούνται από το νερό, εξ αιτίας των υδροστατικών πιέσεων, κάθετες δυνάμεις. Αυτές οι δυνάμεις πίεσης είναι μεγαλύτερες όσο πιο βαθιά μέσα στο νερό βρίσκονται τα αντίστοιχα τμήματα της επιφάνειας. Όλες αυτές οι δυνάμεις δίνουν μια συνισταμένη, που την ονομάζουμε άνωση ό άντωση FA και έχει μέτρο FA = ε x V, όπου ε είναι το ειδικό βάρος του υγρού και V, ο όγκος του σώματος. Θεωρητικά, η άντωση εξασκείται κατακόρυφα, από κάτω προς τα πάνω, σε ένα σημείο (γεωμετρικό κέντρο του σώματος), που λέγεται κέντρο άντωσης. Η πυκνότητα του θαλασσινού νερού (στη Μεσόγειο) είναι 1,027 κιλά ανά κυβικό μέτρο (kg/m³), ενώ του γλυκού είναι 1 κιλό ανά κυβιοκό μέτρο (kg/m³) και εννοούμε πάντα αποσταγμένο νερό, σε 40 βαθμούς Κελσίου και πίεση μιας ατμόσφαιρας.
Ένα σκάφος με εκτόπισμα 10.000 kg. έχει όγκο γάστρας (όγκο εκτοπίσματος Ο), που ισούται με το Βάρος (Β) δια του ειδικού βάρους (ε), δηλαδή 10.000 kg / 1,027 kg/m³ = 9.737 m³, άρα o όγκος Ο = 9.737 m³ (κυβικά μέτρα). Επίσης, εκφράζοντας μια άλλη συνθήκη, μπορούμε να πούμε πως το ίδιο σκάφος υφίσταται μια δύναμη άντωσης FA = ε x V = 1,027 kg/m³ x 9.737 m³ =10.000 kg, που είναι ίση με το βάρος του. Από αυτά μπορούμε να πούμε πως Βάρος = Εκτόπισμα = ?ντωση.
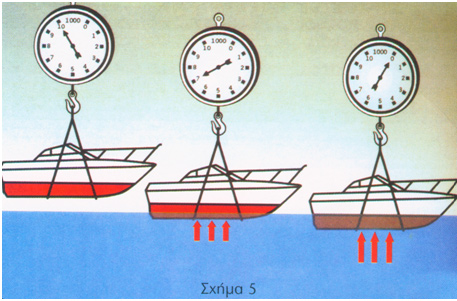
Όλοι έχουμε σίγουρα παρατηρήσει πως είναι ευκολότερο να σηκώσουμε κάποιον άλλο μέσα στο νερό, απΆ ότι έξω στη στεριά. Το σώμα μας μέσα στο νερό χάνει βάρος λόγω του όγκου και της άντωσης. Κάτι παρεμφερές συμβαίνει και με το σκάφος. Ας δούμε ένα ακόμα παράδειγμα. Στο σχήμα 5 έχουμε ένα σκάφος βάρους 10.000 κιλών, έτοιμο να μπει στο νερό. Όταν θα εκτοπίσει βάρος 10.000 κιλά νερού ή έναν όγκο νερού 9.737 κυβικών μέτρων, θα πλεύσει μόνο του και η ζυγαριά θα δείχνει βάρος 0 (μηδέν). Στην κατάσταση αυτή θα υφίσταται μια δύναμη άντωσης ίση με το βάρος του, δηλαδή 10.000 κιλά.
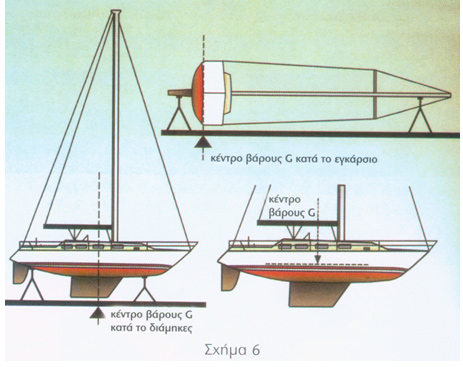
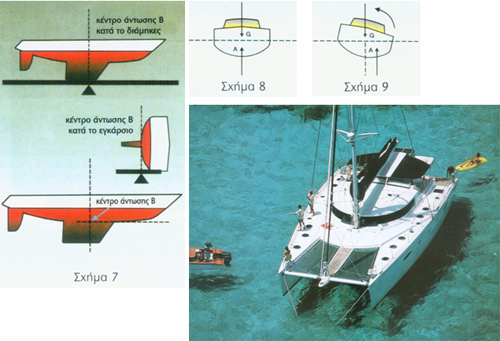
Εφόσον ένα σκάφος πλέει στο νερό (αρχική ευστάθεια) σημαίνει πως σι δυνάμεις βάρους και άντωσης βρίσκονται σε ισορροπία. Όπως ξέρουμε, οι δύο δυνάμεις αυτές είναι το βάρος του σκάφους, που εξασκείται σε ένα σημείο γνωστό ως κέντρο βάρους και η άντωση που, όπως είδαμε, εξασκείται στο γεωμετρικά κέντρο των υφάλων του, γνωστό ως κέντρο άντωσης. Και τα δύο αυτά σημεία βάρους και πλευστότητας είναι θεωρητικά (γεωμετρικά κέντρα βάρους και όγκου) σημεία, όπου εξασκούνται οι συνιστάμενες δυνάμεις όλων των στοιχειωδών μερών του σκάφους. Το κέντρο βάρους G είναι το γεωμετρικά σημείο του βάρους του σκάφους και των μερών που το απαρτίζουν. Αν μπορούσαμε να ισορροπήσουμε ένα σκάφος πάνω σε μια μεγάλη τραμπάλα, κατά την εγκάρσια και διαμήκη έννοια, θα μπορούσαμε να βρούμε τα αντίστοιχα διαμήκη και εγκάρσια κέντρα βάρους όπως φαίνεται στο σχήμα 6. Το κέντρο άντωσης Β είναι το γεωμετρικό κέντρο των υφάλων του σκάφους. Θα μπορούσαμε ακόμα να πούμε πως το κέντρο άντωσης είναι το κέντρο βάρους του νερού, που το σκάφος εκτοπίζει. Αν μπορούσαμε να παγώσουμε για μια στιγμή το νερό που εκτοπίστηκε από το σκάφος και να διατηρήσουμε το σχήμα του «λάκου» που θα άφηνε η γάστρα του σκάφους, θα μπορούσαμε να εφαρμόσουμε την ίδια μέθοδο με τον προσδιορισμό του κέντρου βάρους, βάζοντας τον πάγο πάνω σε μια τεράστια τραμπάλα (σχήμα 7). Έτσι θα μπορούσαμε να βρούμε αντίστοιχα το εγκάρσιο και διάμηκες κέντρο άντωσης.

Για να ισορροπήσει και να πλεύσει ένα σκάφος στο νερό, θα πρέπει οι δυνάμεις βάρους και άντωσης να είναι ίσες και αντίθετες, αλλά και να εξασκούνται στο ίδιο επίπεδο (σχήμα 8). Αν τα κέντρα βάρους και άντωσης διαφοροποιηθούν, είτε με την προσθήκη κάποιου βάρους (κατά την εγκάρσια ή διαμήκη έννοια), είτε με την αλλαγή της θέσης του κέντρου άντωσης λόγω κλίσης του σκάφους από κάποιο κύμα για παράδειγμα, οι δύο δυνάμεις εξασκούνται σε διαφορετικά επίπεδα και δημιουργούν ροπή, που τείνει να επαναφέρει το σκάφος στην οριζόντια θέση (σχήμα 9) ή ακόμα, κάτω από ορισμένες συνθήκες να το ανατρέψει.