Το πηδάλιο του σκάφους και πώς λειτουργεί
Τα σκάφη και τα μυστικά τουςΤου Μάκη Ματιάτου
Τι εννοούμε όταν λέμε πως «δεν ακούει» το τιμόνι; Ποιοι είναι οι παράγοντες, που επηρεάζουν την ανταπόκριση του ιστιοφόρου ή μηχανοκίνητου σκάφους στο πηδάλιο; Πώς συμπεριφέρεται το σκάφος στη στροφή; Αυτά είναι τα ερωτήματα που θα μας απασχολήσουν εδώ, σε μία προσπάθεια να γίνει πιο κατανοητή η ενέργεια του πηδαλίου και η συμπεριφορά του σκάφους, μηχανοκίνητου ή ιστιοφόρου, όταν ταξιδεύουμε.
Σχολές ιστιοπλοΐας και μηχανοκίνησης υπάρχουν πολλές, όπου μπορεί κανείς να πάρει τα απαραίτητα πρώτα εφόδια και γνώσεις για να γίνει -με πολλή βέβαια εξάσκηση- ένας καλός κυβερνήτης. Με το θέμα αυτό φιλοδοξούμε να προσφέρουμε κάτι παραπάνω από τα κλασσικά μαθήματα των σχολών, εξοικειώνοντας τους μελλοντικούς επίδοξους θαλασσινούς αλλά και αρκετούς ήδη έμπειρους κυβερνήτες με ακόμα περισσότερα, άγνωστα ίσως, στοιχεία ναυπηγικής γύρω από το σκάφος αναψυχής. Εδώ θα εξετάσουμε τις δυνάμεις από τις οποίες εξαρτάται η υπακοή του σκάφους στο πηδάλιο και πώς αυτές δημιουργούνται.
Όπως ξέρουμε, το πηδάλιο είναι το μέρος του σκάφους, που μας επιτρέπει να κρατάμε και να ελέγχουμε την πορεία μας στο οριζόντιο επίπεδο, να διευθύνουμε, να στρίβουμε και να μανουβράρουμε. Με το τιμόνι στο κέντρο, η ροή του νερού είναι συμμετρική ως προς τις δύο πλευρές της γάστρας. Τι συμβαίνει όμως, αν γυρίσουμε το τιμόνι από τη μια μπάντα; Τι είναι εκείνο, που κάνει το σκάφος να στραφεί; Ας δούμε τι συμβαίνει, όταν επιχειρούμε να στρίψουμε το σκάφος προς κάποια κατεύθυνση.
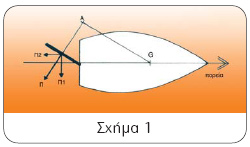
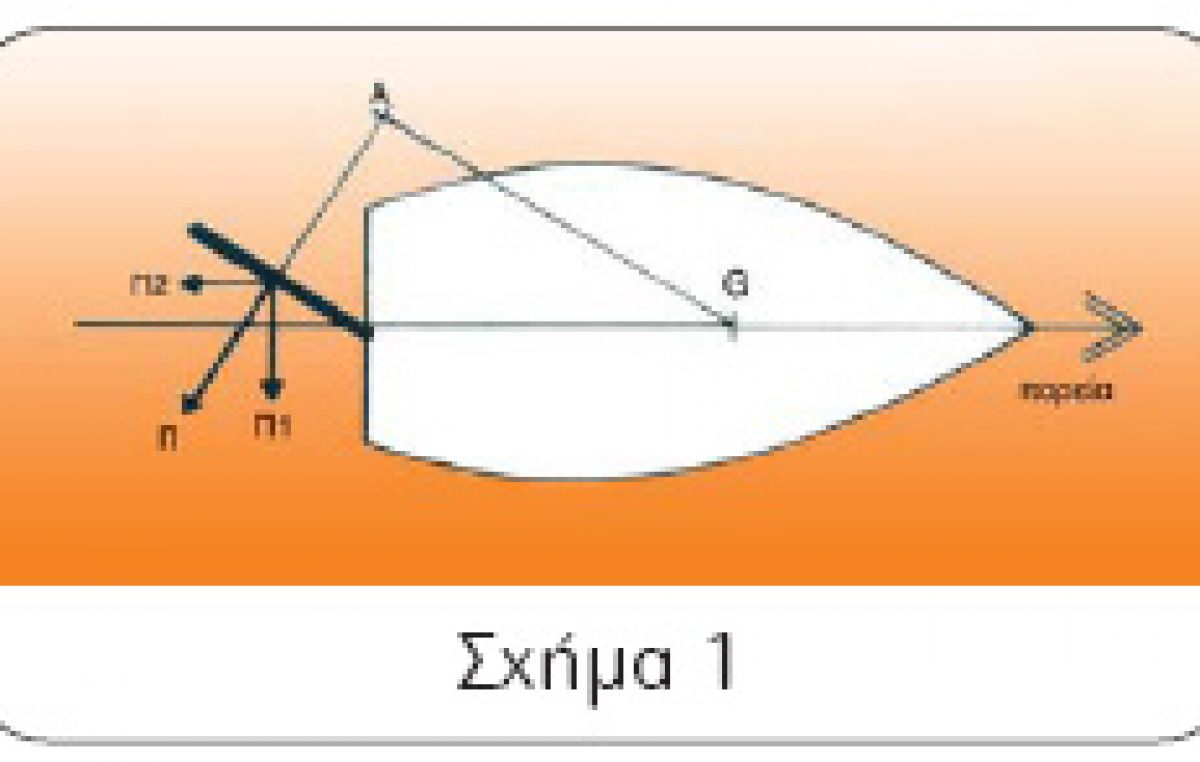
Ο ρόλος του πηδαλίου είναι να δημιουργήσει μια ροπή, που θα στρέψει το σκάφος σε μια γωνία, εκτρέποντάς το έτσι από την αρχική του πορεία. Εδώ θα πρέπει να επισημάνουμε ότι δεν είναι οι δυνάμεις που ασκούνται πάνω στο φτερό του πηδαλίου, εκείνες που θα στρέψουν το σκάφος. Είναι το ίδιο το πηδάλιο, που λειτουργεί σαν ένας σεβρομηχανισμός, ο οποίος το υποχρεώνει να συμπεριφερθεί , έτσι ώστε οι απαραίτητες δυνάμεις και ροπές να δημιουργηθούν υδροδυναμικά με τη ροή του νερού γύρω από τη γάστρα. Αυτός άλλωστε είναι ο λόγος, για τον οποίο η συνολική ευστάθεια πορείας του σκάφους δεν εξαρτάται αποκλειστικά και μόνον από το πηδάλιο, αλλά από την ολική μορφή και το σχήμα της γάστρας. Όταν κατά την πορεία στρίψουμε το τιμόνι (ρόδα ή λαγουδέρα), το φτερό του πηδαλίου παίρνει μια θέση, η οποία σχηματίζει κάποια γωνία με τη ροή του νερού γύρω από τη γάστρα. Το αποτέλεσμα είναι να δημιουργηθεί μια δύναμη, που οφείλεται στην πίεση του νερού πάνω στο πηδάλιο, η οποία τείνει να το επαναφέρει στην αρχική του θέση, δηλαδή παράλληλα με τη ροή του νερού. Αν, για παράδειγμα, αφήσουμε το τιμόνι ελεύθερο, το σκάφος θα γυρίσει σε μια ευθεία πορεία, αφού το πηδάλιο επανέλθει στην αρχική θέση του. Το «ζόρι» αυτό του τιμονιού πάνω στη στροφή ή τη μανούβρα το έχουμε όλοι μας αισθανθεί στα ταξίδια μας, όταν τιμονεύουμε. Στο σχήμα 1 βλέπουμε ένα σκάφος, του οποίου το πηδάλιο έχει πάρει κάποια γωνία ως προς τη ροή του νερού στη γάστρα. Η δύναμη Π που εξασκείται στο πηδάλιο, προσπαθώντας να το επαναφέρει στην αρχική θέση, μπορεί να αναλυθεί στις δύο συνιστώσες της Π1 και Π2. Η Π1 που είναι κάθετη στη ροή, προκαλεί μια ροπή που τείνει να «σπρώξει» την πρύμη πλάγια και να την κάνει να στραφεί με κέντρο το G, δηλαδή το κέντρο βάρους του σκάφους. Η δεύτερη συνιστώσα Π2 που είναι παράλληλη με τη ροή, αλλά αντίθετη προς την πορεία του σκάφους, προκαλεί μια επιβράδυνση, την οποία παρατηρούμε στην πράξη κατά τη στροφή (αντίσταση πηδαλίου). Ας δούμε λοιπόν πώς λειτουργούν αυτές οι δυνάμεις.
Στιγμιαία ανάπτυξη δυνάμεων
Η πρώτη δύναμη Π1 που δημιουργεί τη ροπή, προκαλεί μια παρέκκλιση του σκάφους από την αρχική του πορεία, με αποτέλεσμα αυτό να βρίσκεται σε κάποια δεδομένη στιγμή υπό γωνία με τη ροή του νερού, που λέγεται γωνία εκτροπής. Η παρέκκλιση αυτή δημιουργεί ένα συνδυασμό δυνάμεων, όπως φαίνεται στο σχήμα 2, που προέρχονται από τη ροή του νερού πάνω στη γάστρα. Ας παρακολουθήσουμε τη στιγμιαία αυτή ανάπτυξη των δυνάμεων στο σχήμα 2.
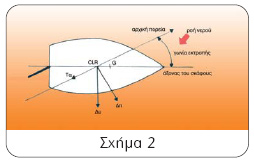
Η υδροδυναμική δύναμη Δυ δρα στο κέντρο πλευρικής αντίστασης CLR (Centre of Lateral Resistance) του σκάφους και έχει την τάση να το επιβραδύνει. Παράλληλα, η Δυ προκαλεί και μια ροπή στρέψης με κέντρο το κέντρο βάρους G του σκάφους. Αν αναλύσουμε τη Δυ στις δύο συνιστώσες της Δπ και Τα, βλέπουμε ότι η πρώτη (Δπ) είναι κάθετη στην αρχική πορεία του σκάφους και σΆ αυτήν οφείλεται η γωνία κλίσης, το γέρσιμο του σκάφους που παρατηρούμε κατά τη στροφή. Η δεύτερη (Τα) είναι η οπισθέλκουσα δύναμη, δηλαδή η συνολική αντίσταση που προξενεί το νερό κατά την κίνηση του σκάφους μέσα στη θάλασσα. Από τα παραπάνω μπορούμε να συμπεράνουμε ότι, η Δυ είναι η δύναμη, που κάνει το σκάφος να ακολουθεί μια κυκλική πορεία, ενώ το πηδάλιο αποτελεί απλώς το «διορθωτικό» μέσον, ώστε να διατηρηθεί η γωνία εκτροπής στη στιγμιαία ροή του νερού.
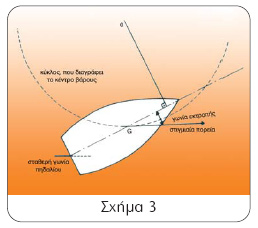
Στο σχήμα 3 μπορούμε να δούμε αναλυτικά τη γωνία εκτροπής του σκάφους, που δεν είναι άλλη από τη σταθερή γωνία, η οποία δημιουργείται κατά τη διάρκεια της παρεκτροπής του σκάφους από τη διεύθυνση της ροής, όταν όλες οι δυνάμεις και ροπές στη γάστρα βρίσκονται σε ισορροπία. Το πόσο αποτελεσματικό είναι το πηδάλιο, εξαρτάται από πολλούς παράγοντες, όπως η επιφάνειά του, η αναλογία όψης του (aspect ratio), ο σχεδιασμός της τομής του και γενικότερα ο συνολικός σχεδιασμός του σκάφους σε σχέση με τη θέση του. Ας δούμε όμως αναλυτικά τους παραπάνω παράγοντες.
Επιφάνεια
Η αρχική δύναμη που ασκείται στο φτερό του πηδαλίου κατά τη στροφή είναι ανάλογη με την επιφάνειά του. Για παράδειγμα, αν ένα πηδάλιο έχει διπλάσια επιφάνεια από κάποιο άλλο του ιδίου γεωμετρικού σχήματος και η γωνία με τη ροπή είναι ίδια, τότε η δύναμη που θα ασκηθεί από το πρώτο θα είναι διπλάσια.
Αναλογία όψης
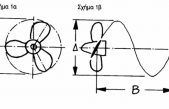
Είναι ο λόγος μεταξύ του μέγιστου πλάτους και του μέγιστου βυθίσματος. Ένα πηδάλιο με υψηλό aspect ratio είναι βαθύ και στενό, ενώ αντίθετα ένα με χαμηλή αναλογία όψης είναι ρηχό και φαρδύ, όπως φαίνεται στο σχήμα 4.
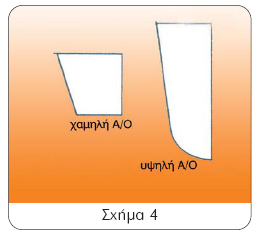
Ένα πηδάλιο με χαμηλή αναλογία όψης μπορεί να λειτουργήσει αποτελεσματικά σε μεγάλες γωνίες, αλλά η δύναμη που χρειάζεται για να τεθεί σε γωνία είναι μεγάλη. Αντίθετα, ένα πηδάλιο με υψηλή αναλογία όψης δεν μπορεί να λειτουργήσει αποτελεσματικά σε μεγάλες γωνίες (δημιουργεί μεγάλες αντιστάσεις χωρίς πρακτικά να στρίβει το σκάφος) αλλά χρειάζεται πολύ μικρότερη δύναμη για να τεθεί υπό γωνία με τη ροή του νερού. Από τα παραπάνω μπορούμε να συμπεράνουμε πως το ιδανικό πηδάλιο για ένα ιστιοφόρο πρέπει να έχει υψηλή αναλογία όψης, ενώ για ένα μηχανοκίνητο χαμηλή.
Πλάγια όψη
Ο σχεδιασμός της πλάγιας όψης πρακτικά δεν έχει σχέση με την άνωση (lift), που δημιουργεί το πηδάλιο και έχει σχετικά μικρή επίδραση στη θέση του κέντρου πίεσής του. Οι λόγοι για τους οποίους έχει σημασία η πλάγια όψη είναι:
α. Να μειώσει στο ελάχιστο το κενό μεταξύ φτερού και γάστρας, ώστε να μην υπάρχουν απώλειες από το στροβιλισμό νερού στο διάκενο.
β. Να μειωθούν οι πιέσεις στο κάτω άκρο του, ώστε οι ροπές με κέντρο τη βάση του πηδαλίου να είναι ελάχιστες και η βάση του να μην υφίσταται κοπώσεις.
Τομή
Το φτερό πρέπει να έχει σχήμα αεροτομής, ώστε να μειωθεί στο ελάχιστο η απώλεια λόγω τριβών. Με υδροδυναμικό σχήμα, η ροή «χαϊδεύει» ομαλά την επιφάνειά του και δεν δημιουργούνται πολλές δίνες, οι οποίες αυξάνουν την αντίσταση (σχήμα 5).
Συνδυασμός σκάφους και πηδαλίου
Δύο είναι οι σημαντικότεροι παράγοντες, που επηρεάζουν την απόδοση του πηδαλίου σε σχέση με τη θέση της τοποθέτησής του. Πρώτον η κάθετη απόστασή του από το κέντρο βάρους του σκάφους και δεύτερον η θέση του, ώστε η ροή του νερού γύρω του να είναι όσο το δυνατόν πιο ομαλή, άρα πιο αποτελεσματική. Η ιδανική θέση του τιμονιού είναι το σημείο, όπου θα μπορεί να δημιουργηθεί η μεγίστη ροπή περιστροφής, με κέντρο το κέντρο βάρους του σκάφους και απόσταση από το κέντρο πίεσης του πηδαλίου όσο γίνεται πιο μεγάλη (σχήμα 6).

Η ροή του νερού που δέχεται στο πηδάλιο ένα ιστιοφόρο, διαφέρει από αυτήν του μηχανοκίνητου σκάφους. Σε ένα μηχανοκίνητο η ροή είναι αρκετά ομαλή, αφού συνήθως δεν υπάρχουν στοιχεία και προεξοχές, όπως καρίνα, skeg κ.λπ., που προκαλούν δίνες. Η ταχύτητα επίσης της ροής στο μηχανοκίνητο είναι αρκετή για να δημιουργήσει την αρχική πίεση στο φτερό, αφού συνήθως βρίσκεται πολύ κοντά στην προπέλα. Στην περίπτωση του ιστιοφόρου, η καρίνα και το skeg προκαλούν μια παρεκτροπή στη ροή, μια και αυτή δεν είναι παράλληλη με την πορεία του σκάφους αλλά υπό κάποια γωνία, όπως φαίνεται στο σχήμα 7. Γενικά μπορούμε να πούμε πως η ιδανική θέση για το τιμόνι είναι αυτή, όπου η ροή γύρω του είναι όσο γίνεται πιο ομαλή.

Απόδοση πηδαλίου
Για να εμβαθύνουμε περισσότερο στο θέμα μας θα πρέπει να αναφερθούμε σε μερικούς απλούς ναυπηγικούς όρους, που θα βοηθήσουν στην κατανόηση της λειτουργίας του πηδαλίου. Υπάρχουν διάφορες μέθοδοι, με τις οποίες μπορούμε να μελετήσουμε την απόδοση του τιμονιού σε ένα σκάφος. Η πιο αποτελεσματική και ευρύτερα αποδεκτή είναι αυτή της περιστροφής κύκλου, κατά την οποία το σκάφος διαγράφει μια πλήρη περιστροφή 360ο.
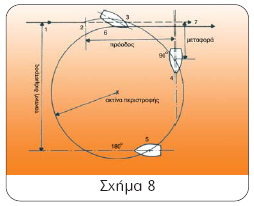
Ας παρακολουθήσουμε στο σχήμα 8 τις διαδοχικές φάσεις μιας τέτοιας περιστροφής.
1. Το σκάφος βρίσκεται στην αρχική του πορεία.
2. Γυρίζουμε το τιμόνι και το κρατάμε σε μια σταθερή γωνία.
3. Το σκάφος μας κινείται με μια πλάγια έκπτωση και ελαφρά κλίση, η ταχύτητά του μειώνεται και η πορεία του αλλάζει με τις ροπές που δημιουργούνται.
4. Η αρχική πορεία αλλάζει κατά 90ο . Η απόστασή του παράλληλα με την αρχική πορεία είναι η λεγόμενη μετατόπιση ή πρόοδος (advance). Η απόστασή του κάθετα με την αρχική πορεία είναι η προχώρηση ή μεταφορά (transfer). Αυτό είναι και το στοιχείο, που μας δίνει την ανταπόκριση του σκάφους στο τιμόνι, δηλαδή αυτό που λέμε στη ναυτική διάλεκτο «πόσο ακούει το τιμόνι».
5. Το σκάφος τώρα κινείται παράλληλα προς την αρχική του πορεία, σε αντίθετη όμως κατεύθυνση. Η κάθετη απόσταση από την αρχική του πορεία λέγεται τακτική διάμετρος. Η διάμετρος της περιφέρειας, που σχηματίζει το κέντρο βάρους του σκάφους, λέγεται τελική διάμετρος ή ακτίνα περιστροφής (steady radius of turn). Οι παραπάνω τρεις αποστάσεις, δηλαδή η πρόοδος, η μεταφορά και η τακτική διάμετρος είναι τα μέτρα απόδοσης του τιμονιού. Όσο μικρότερες είναι οι τιμές τους, τόσο πιο αποτελεσματικό θεωρείται το πηδάλιο.
Τύποι πηδαλίων
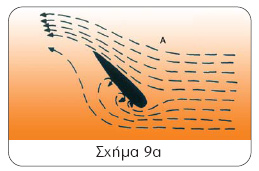
Πριν κλείσουμε το θέμα μας, καλό θα είναι να δούμε και τους πλέον συνηθισμένους τύπους και μορφές πηδαλίων, που παίρνουν το όνομά τους από το σχήμα και τον τρόπο λειτουργίας τους. Υπάρχουν πηδάλια ορθογώνια με ελαφρά στρογγυλεμένη την πρυμιά κάτω γωνία, τραπεζοειδή ή ακόμα και ελλειπτικά, που συναντάμε κυρίως στα σύγχρονα ιστιοφόρα. Το πτερύγιο του πηδαλίου μπορεί να είναι το γνωστό κοινό πηδάλιο, που στρέφεται γύρω από τα βελόνια (σχήμα 9Α),
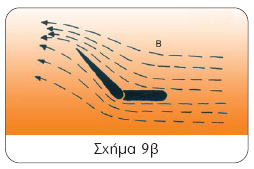
η το κοίλο ή υδροδυναμικό πηδάλιο, που με τη βοήθεια ποδοστήματος (skeg) δημιουργεί μια υδροδυναμική τομή στη ροή του νερού (σχήμα 9Β). Όπως φαίνεται στο σχήμα 9, το φτερό Β διευκολύνει την ομαλή ροή, με αποτέλεσμα το σκάφος να μην έχει απώλειες σε ταχύτητα. Ένας άλλος ορισμός του πηδαλίου είναι αυτός που εξαρτάται από την κατανομή του κέντρου εφαρμογής της δύναμης από τον άξονα περιστροφής του.
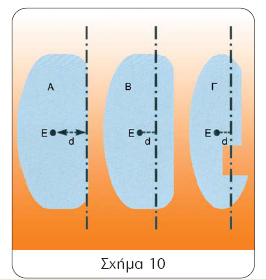
Στο σχήμα 10 βλέπουμε τρεις τύπους πηδαλίων, το κοινό πηδάλιο (Α), το ζυγοσταθμισμένο (Β) και το ημιζυγοσταθμισμένο (Γ), όπου με Ε σημειώνεται το κέντρο εφαρμογής της δύναμης και με d η απόσταση του Ε από τον άξονα. Όσο πιο μικρή είναι η απόσταση d, τόσο πιο μικρή είναι και η ροπή στρέψης του (Exd), άρα και τόσο πιο ελαφρύ είναι. Το ζυγοσταθμισμένο πηδάλιο παρουσιάζει αισθητή διαφορά από τους άλλους τύπους, όχι μόνον από άποψη κατασκευής, διάταξης, ανάρτησης και προσαρμογής του στην πρύμη, αλλά και από άποψη ενέργειας, γιατί η έλλειψη του skeg επιτρέπει τη διαφυγή του νερού από το πλωριό τμήμα του. Το πηδάλιο αυτού του τύπου λειτουργεί ουσιαστικά σαν μια ελεύθερη ή φέρουσα επιφάνεια κατά την έννοια των κανόνων της υδροδυναμικής, χωρίς δηλαδή τη συνεργασία του ποδοστήματος ή της ουράς της γάστρας.
Πρόβλεψη απόδοσης πηδαλίων
Η πρόβλεψη της απόδοσης του τιμονιού είναι ένα αρκετά πολύπλοκο τεχνικό θέμα, που όμως πιστεύουμε θα ενδιαφέρει πολλούς κυβερνήτες σκαφών αναψυχής με κάποιες τεχνικές γνώσεις. Ας επιχειρήσουμε λοιπόν μια σύντομη -και όσο πιο απλοποιημένη γίνεται- αναφορά στο θέμα. Η απόδοση του τιμονιού είναι προβλέψιμη από το αρχικό στάδιο της σχεδίασης ενός σκάφους, μηχανοκίνητου ή ιστιοφόρου. Σύμφωνα με έρευνες Αμερικανών επιστημόνων τα τελευταία χρόνια, προτείνεται η παρακάτω διαδικασία. Αρχικά θα πρέπει να γίνει κάποια εκτίμηση της μείωσης της ταχύτητας κατά τη διάρκεια της στροφής του σκάφους.
Η διαδικασία είναι η ακόλουθη:
1. Εκτίμηση της αντίστασης από τα ύφαλα του σκάφους για ένα φάσμα ταχυτήτων, συμπεριλαμβάνοντας και την αντίσταση του πηδαλίου σε γωνία 0ο από την πορεία του σκάφους.
2. Εκτίμηση της αντίστασης, που δημιουργείται από το πηδάλιο για ένα φάσμα γωνιών στις συγκεκριμένες ταχύτητες.
3. Υπολογισμός της διαφοράς μεταξύ της αντίστασης του πηδαλίου σε κάθε γωνιά και της αντίστασής του σε μηδενική γωνία.
4. Εκτίμηση της πρόσθετης αντίστασης που δημιουργείται λόγω του ότι το σκάφος παίρνει κάποια κλίση κατά τη διάρκεια της στροφής.
5. Για κάθε συγκεκριμένη γωνία του πηδαλίου προσθέτουμε την αντίσταση λόγω της γωνίας του πηδαλίου με το νερό (από το βήμα 3) στην πρόσθετη αντίσταση λόγω της κλίσης κατά τη διάρκεια της στροφής (από το βήμα 4), έτσι ώστε να βρεθεί η ολική αντίσταση του σκάφους κατά τη διάρκεια της στροφής.
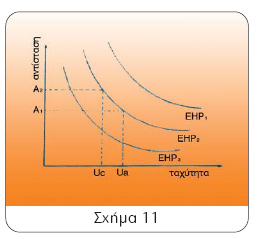
6. Με την προϋπόθεση ότι, η κινητήριος δύναμη (με πανιά ή μηχανή) παραμένει σταθερή κατά τη διάρκεια της στροφής και ότι η ταχύτητα, που έχει το σκάφος πριν από τη στροφή είναι Ua, τότε η ταχύτητα του σκάφους κατά τη διάρκεια της στροφής Uc μπορεί να υπολογισθεί από το διάγραμμα Αντίστασης/ Ταχύτητας. Οπότε ο λόγος Uc/Ua μπορεί επίσης να υπολογισθεί. Μετά από πειράματα έχει αποδειχθεί ότι ισχύει η παρακάτω σχέση:
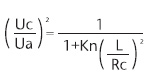
Με κατάλληλες μετατροπές στην παραπάνω εξίσωση, ο ρυθμός στροφής Uc/Rc (rate of turn) ισούται με:
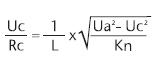
Όπου L= μήκος σκάφους, Rc= ακτίνα περιστροφής, Uc= σταθερή ταχύτητα κατά τη διάρκεια της στροφής, Ua= ταχύτητα πριν από τη στροφή και Kn = σταθερά απόδοσης πηδαλίου. Επίσης η σταθερά απόδοσης του πηδαλίου ισούται με:
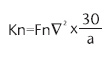
Όπου Fη= σταθερά ταχύτητας/εκτοπίσματος και α=γωνία πηδαλίου σε μοίρες.
Για τα σχήματα
Σχήμα 1
Π Π1 Π2 Α G πορεία
Σχήμα 2
Τα CLR G Δυ Δπ αρχική πορεία ροή νερού γωνία εκτροπής άξονας του σκάφους
Σχήμα 3
κύκλος που διαγράφει το κέντρο βάρους
σταθερή γωνία πηδαλίου γωνία εκτροπής στιγμιαία πορεία G O
Σχήμα 4
χαμηλή Α/Ο υψηλή Α/Ο
Σχήμα 5
δίνες γύρω από το πηδάλιο
περιοχή όπου δημιουργούνται δίνες
Σχήμα 6
κέντρο βάρους
κέντρο πίεσης πηδαλίου
Σχήμα 7
πηδάλιο καρίνα
Σχήμα 8
τακτική διάμετρος πρόοδος μεταφορά ακτίνα περιστροφής
1 2 3 4 5 6 7 180° 90°
Σχήμα 9α
Α
Σχήμα 9β
Β
Σχήμα 10 Α Β Γ
Ε d Ed Ed
Σχήμα 11
αντίσταση Α1 Α2 Uc Ua ταχύτητα EHP1 EHP2 EHP3