Μετρήστε την ευστάθεια του σκάφους σας
Τα σκάφη και τα μυστικά τουςΜετρήστε την ευστάθεια του σκάφους σας
Μια πρακτική εφαρμογή του πειράματος ευστάθειας για μηχανοκίνητα και ιστιοφόρα σκάφη αναψυχής
Του Μάκη Ματιάτου
Ακούμε, κατά καιρούς, διάφορους κατά τα άλλα έμπειρους φίλους της θάλασσας να αναφέρονται σε θέματα ευστάθειας, με την πρακτική της έννοια. Πόσοι, όμως, επεχείρησαν να «μετρήσουν» την ευστάθεια του σκάφους τους;
Θέλοντας να απομυθοποιήσουμε, λοιπόν, την έννοια της ευστάθειας και να τη θέσουμε σε μια πρακτική βάση, θα αναφερθούμε στη θεωρία της και στη συνέχεια στην εφαρμογή ενός πειράματος ευστάθειας, που μπορείτε να κάνετε μόνοι σας, στο μηχανοκίνητο ή ιστιοφόρο σκάφος σας. Είναι εξαιρετικά δύσκολο να αναλύσουμε όρους και έννοιες, όπως η ευστάθεια, χωρίς να πελαγοδρομήσουμε σε ευρύτερα στοιχεία της ναυπηγικής. Άλλωστε, το θέμα της ευστάθειας δεν θα μπορούσε να εξαντληθεί μέσα σε μερικές σελίδες. Εδώ, θα προσπαθήσουμε να σας «ξεναγήσουμε» σύντομα, όσο γίνεται πιο «ανώδυνα» και με τη χρήση στοιχειωδών μαθηματικών και φυσικής, στη μαγεία των σκαφών αναψυχής, μηχανοκίνητων και ιστιοφόρων, και στα σύνθετα κέντρα τους, για να κάνουμε την έννοια «ευστάθεια» περισσότερο κατανοητή.
Επειδή το σκάφος κινείται στο χώρο των τριών διαστάσεων, υπάρχουν τρεις
διαφορετικοί προσδιορισμοί του όρου «ευστάθεια», ανάλογα με το επίπεδο στο οποίο αναφερόμαστε. Υπάρχουν ας πούμε τρεις «ευστάθειες», που χαρακτηρίζουν την κατάσταση του σκάφους, η διαμήκης (longitudinal stability), η εγκάρσια (transverse stability) και η ευστάθεια πορείας (directional stability). Για να μην επεκταθούμε πολύ στην κίνηση του σκάφους μέσα στο νερό, ας δούμε τις τρεις αυτές ευστάθειες στο σχήμα 1. Όταν το σκάφος ταξιδεύει, κινείται σε τρία επίπεδα και ως εκ τούτου κάνει τρεις κινήσεις:
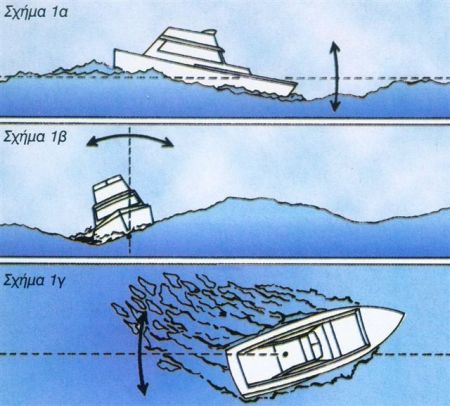
Σκαμπανέβασμα (σχ. 1α) (πρόνευση, pitch), είναι η κατά το διάμηκες ταλάντωση, δηλαδή μία κυκλική κίνηση γύρω από τον εγκάρσιο άξονά του, που συνδέεται με τη διαμήκη ευστάθεια.
Μπότζι (σχ. 1β) (διατοίχιση, roll), είναι η κατά το διαμήκη άξονά του κυκλική ταλάντωση. Αυτή είναι και η κίνηση του σκάφους που συνδέεται άμεσα με την εγκάρσια ευστάθεια, την οποία θα εξετάσουμε εδώ. Είναι η πιο βασική κίνηση, που επηρεάζει κυρίως την ασφάλεια του σκάφους. Επίσης, η κίνηση αυτή, σε συνδυασμό με την περίοδο της ταλάντωσης, είναι υπεύθυνη και για τη ναυτία.
Έκπτωση (σχ. 1γ) (yaw) είναι η ταλάντωση γύρω από το κέντρο βάρους του σκάφους, στο επίπεδο της ισάλου επιφανείας και αφορά την ευστάθεια πορείας.
Οι παραπάνω τρεις κυκλικές ταλαντώσεις δεν είναι οι μόνες, που παρατηρούνται στο σκάφος. Υπάρχουν ακόμα τρεις δευτερεύουσες γραμμικές ταλαντώσεις του κέντρου βάρους του σκάφους, που δημιουργούνται σε συνδυασμό με τις βασικές κυκλικές ταλαντώσεις και είναι οι παρακάτω, όπως φαίνονται στο σχήμα 2:
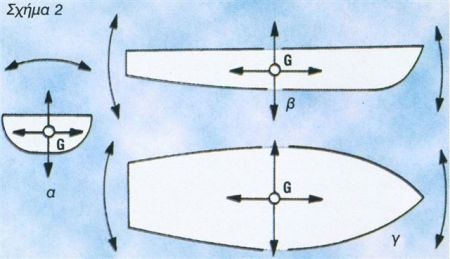
Σχήμα 2α.
Παρατηρούμε ότι το κέντρο βάρους G κινείται με μία γραμμική ταλάντωση πάνω-κάτω (heave), που προκαλείται από το σκαμπανέβασμα, αλλά και με μία άλλη δεξιά-αριστερά (sway).
Σχήμα 2β.
Παρατηρούμε μία γραμμική ταλάντωση του G πάνω-κάτω (heave), που είδαμε στα σχήμα 2α, αλλά συγχρόνως και μία ταλάντωση κατά το διάμηκες (surge), δηλαδή εμπρός-πίσω, που προκαλείται από το καβάλημα στο κύμα και προκαλεί επιβράδυνση στο ανέβασμα ή επιτάχυνση στο κατέβασμα από την κορυφή του κύματος.
Σχήμα 2γ.
Εδώ έχουμε το συνδυασμό των δύο γραμμικών ταλαντώσεων του G κατά μήκος του εγκάρσιου άξονα (sway) και του διαμήκους άξονα (surge).
Τις τρεις γραμμικές ταλαντώσεις του σκάφους μπορούμε εύκολα να
παρατηρήσουμε, όταν είμαστε δεμένοι στο μώλο και έρχονται απόνερα. Εκείνο επίσης, που παρατηρούμε εξετάζοντας την κίνηση του σκάφους στο νερό είναι ότι κάθε μία από τις βασικές κυκλικές ταλαντώσεις συνδυάζεται πάντα με δύο γραμμικές ταλαντώσεις του κέντρου βάρους G του σκάφους, που ολοκληρώνουν τη έννοια της ελεύθερης κίνησής του στο επίπεδο της παρατήρησης.
Όπως διαπιστώσαμε με τα παραπάνω, η εγκάρσια ευστάθεια είναι εκείνη, που θα πρέπει να μας απασχολήσει, μια και επηρεάζει την ασφάλεια της
πλεύσης μας. Εγκάρσια ευστάθεια λέγεται η ιδιότητα του σκάφους να
αντιστέκεται στην κλίση, αλλά και αφού πάρει κάποια κλίση, να επανέρχεται στην αρχική οριζόντια θέση του και να πλέει στη φυσική του ίσαλο. Η τάση να αντιστέκεται στην κλίση λέγεται αρχική ευστάθεια, ενώ αυτή της επαναφοράς του ευστάθεια κλίσης. Με τον όρο δυναμική ευστάθεια εννοούμε το
μηχανικό έργο, που πρέπει να καταβληθεί για να πάρει το σκάφος μία
ορισμένη γωνία κλίσης ή για να επανέλθει από μία κεκλιμένη θέση στην
οριζόντια. Οι παραπάνω αυτές έννοιες μας είναι απαραίτητες για να
κατανοήσουμε στη συνέχεια την εγκάρσια ευστάθεια και το πείραμα ευστάθειας, που θα επιχειρήσουμε.
Το ιστιοφόρο σκάφος είναι ένα πιο σύνθετο ναυπήγημα από το μηχανοκίνητο, επειδή επηρεάζεται από τον αέρα, που πέφτει στα πανιά του. Εδώ, λοιπόν, θα κάνουμε μία μικρή παρέκκλιση για τους φίλους του ιστιοφόρου, εξετάζοντας τα διάφορα κέντρα που επηρεάζουν την εγκάρσια ευστάθειά του, πριν μπούμε στο πείραμα ευστάθειας, που αφορά όλα ανεξαρτήτως τα σκάφη. Όσοι δεν ενδιαφέρονται να παρακολουθήσουν τι συμβαίνει με το ιστιοφόρο, μπορούν να συνεχίσουν από την παράγραφο, που αναφέρεται παρακάτω στα κέντρα άντωσης και βάρους.
Κέντρο ιστιοφορίας και πλευρικής αντίστασης του ιστιοφόρου
Το ιστιοφόρο σκάφος έχει δύο βασικά κέντρα, που επηρεάζουν την ευστάθειά του. Πρόκειται για το κέντρο ιστιοφορίας (center of effort, CE) και το κέντρο πλευρικής αντίστασης (center of lateral resistance, CLR). Η απόσταση των δύο αυτών κέντρων είναι το ζητούμενο στην περίπτωση ενός ιστιοφόρου. Θα
προσπαθήσουμε, λοιπόν, να βρούμε πρακτικά και χωρίς πολύπλοκους υπολογισμούς, πρώτα το κέντρο ιστιοφορίας και την απόστασή του από την ίσαλο και στη συνέχεια, πάλι με εμπειρικό τρόπο, το κέντρο πλευρικής αντίστασης και την απόστασή του επίσης από την ίσαλο, για να μπορέσουμε να υπολογίσουμε κατά προσέγγιση την απόσταση μεταξύ των δύο κέντρων. Το μόνο που χρειαζόμαστε είναι ένα σχέδιο ιστιοφορίας και πλάγιας όψης (προφίλ) του σκάφους μας, που μπορούμε να βρούμε σε όλα τα διαφημιστικά φυλλάδια σε κλίμακα.
Κέντρο ιστιοφορίας ή κέντρο πρόσπτωσης ενός τριγωνικού πανιού είναι το γεωμετρικό του κέντρο, δηλαδή το σημείο τομής των διαμέσων του τριγώνου (σχ. 3). Για να υπολογίσουμε το κέντρο ιστιοφορίας, για παράδειγμα ενός sloop, από το πλάνο ιστιοφορίας του βρίσκουμε ξεχωριστά τα κέντρα των δύο βασικών πανιών του, τα οποία στη συνέχεια ενώνουμε με μία ευθεία (σχ. 4). Μετά, φέρουμε δύο καθέτους προς την ίσαλο, που να περνούν από τα δύο κέντρα πρόσπτωσης των δύο πανιών, στη μεν μεγίστη, από το σημείο πρόσπτωσης και κάτω, στο δε πλωριό πανί, προς τα πάνω (σχ. 5). Προσοχή, το πλωριό πανί υπολογίζεται σαν το πλωριό τρίγωνο, δηλαδή σαν μία τζένοα 100%, που η ποδιά της δεν ξεπερνά τη σκάντζα (βάση του καταρτιού).
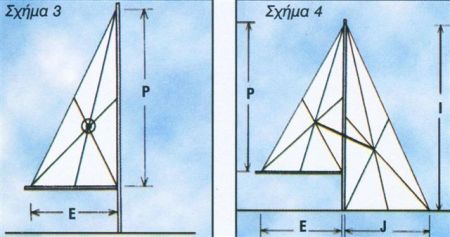
Απόσταση κέντρου ιστιοφορίας από την ίσαλο
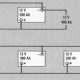
Αν, για παράδειγμα, το εμβαδόν της μαΐστρας είναι 25 τ.μ. και του πλωριού πανιού 30 τ.μ., τότε το εμβαδόν ιστιοφορίας είναι το άθροισμα των δύο επιφανειών, δηλαδή 55 τ.μ. Χαράζουμε, λοιπόν, μία ευθεία σε μία τυχαία κλίμακα (αναλογικά), την οποία σημειώνουμε ανά 0,5 εκατοστά. Με την ευθεία αυτή σαν κλίμακα, χαράζουμε κάποιο σημείο στην κάθετο της μεγίστης, που απέχει 3 εκατοστά (αναλογία του εμβαδού του πλωριού πανιού 30 τ.μ = 3 εκατοστά) από το κέντρο πρόσπτωσης προς τα κάτω. Αντίστοιχα σημειώνουμε το ανάλογο σημείο πάνω στην κάθετο του πλωριού πανιού προς τα πάνω (αναλογία του εμβαδού της μαΐστρας 25 τ.μ. = 2,5 εκατοστά). Στη συνέχεια ενώνουμε τα δύο σημεία με μία ευθεία, που τέμνει την άλλη ευθεία μεταξύ των δύο κέντρων πρόσπτωσης των πανιών, όπως φαίνεται στο σχήμα 5. Το σημείο τομής είναι θεωρητικά το κέντρο ιστιοφορίας του σκάφους του παραδείγματός μας. Στο σχέδιο ιστιοφορίας μετράμε την απόστασή του από την ίσαλο σχεδίασης.
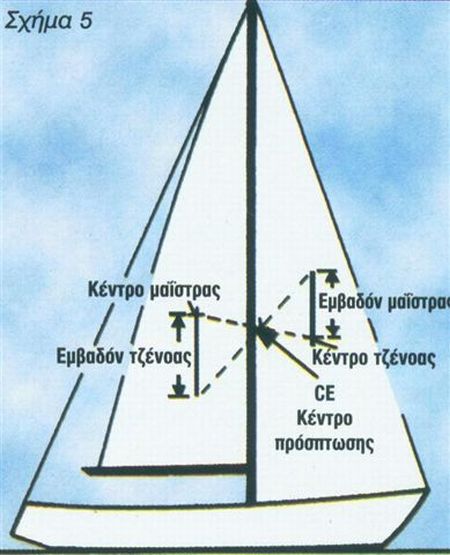
Απόσταση κέντρου πλευρικής αντίστασης από την ίσαλο
Με πρακτικό τρόπο μπορούμε να βρούμε επίσης το κέντρο πλευρικής αντίστασης και να μετρήσουμε την απόστασή του από την ίσαλο. Από την πλάγια όψη του σκάφους αποτυπώνουμε σε ένα χαρτόνι το σχήμα των υφάλων του σκάφους, χωρίς όμως το φτερά του πηδαλίου. Στη συνέχεια το κόβουμε και το ισορροπούμε πάνω σ? ένα χάρακα, κατά την εγκάρσια και διαμήκη έννοια, όπως φαίνεται στο σχήμα 6.
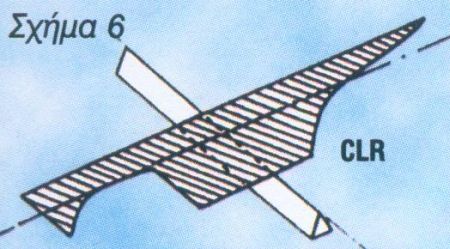
Το κέντρο πλευρικής αντίστασης είναι το γεωμετρικά κέντρο των υφάλων του σκάφους. Βρίσκοντας το σημείο τομής των δύο ευθειών της ισορρόπησης, μετράμε εύκολα την απόστασή του από την ίσαλο. Γενικά και χάριν υπολογισμού δεχόμαστε πως στην περίπτωση ενός ιστιοφόρου, βρίσκεται κάτω από την ίσαλο, σε μία απόσταση περίπου 40% του βυθίσματος.
Έχοντας γνωρίσει τα δύο βασικά κέντρα ιστιοφορίας και πλευρικής αντίστασης και την απόσταση μεταξύ τους, είμαστε έτοιμοι να υπολογίσουμε την αρχική εγκάρσια ευστάθεια του σκάφους. Αφού εξετάσουμε και τα
υπόλοιπα δεδομένα, θα μπορέσουμε να δούμε και τι συμβαίνει με τις μεγάλες κλίσεις, που ειδικά ένα ιστιοφόρο μπορεί να αποκτήσει, με την καμπύλη ευστάθειας.
Ροπή κλίσης και ευστάθειας
Όπως φαίνεται στο σχήμα 7, η αεροδυναμική δύναμη που εξασκείται στο κέντρο ιστιοφορίας CE και η υδροδυναμική δύναμη στο κέντρο πλευρικής αντίστασης CLR δημιουργούν ένα ζεύγος δυνάμεων με μοχλοβραχίονα τη μεταξύ τους απόσταση, που υπολογίσαμε παραπάνω (απόσταση CE από CLR). Επειδή η αεροδυναμική δύναμη είναι ίση με την υδροδυναμική, η ροπή που δημιουργείται, τείνει να δώσει κάποια κλίση στο σκάφος. Το γεγονός ότι το σκάφος δεν αναποδογυρίζει σημαίνει πως δημιουργείται μία άλλη ροπή, ίση και αντίρροπη (με διαφορετική φορά) με την πρώτη, που τείνει να επαναφέρει τα σκάφος στην οριζόντια θέση του ώστε να πλεύσει στη φυσική του ίσαλο. Η πρώτη ροπή είναι η λεγόμενη ροπή κλίσης, ενώ η δεύτερη, η ροπή ευστάθειας, Όπως είπαμε, οι δύο ροπές είναι ίσες και αντίρροπες. Ας δούμε τώρα τα κέντρα, που μας αφορούν.
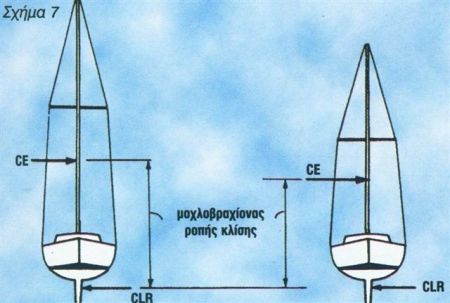
Κέντρα άντωσης και βάρους
Ένα σκάφος λέμε ότι ισορροπεί, όταν πλέει σε οριζόντια θέση. Στην κατάσταση αυτή μας ενδιαφέρουν τα δύο βασικά κέντρα άντωσης ή πλευστότητας (center of buoyancy, Β) και κέντρο βάρους (center of gravity, G). Εφόσον ένα σκάφος πλέει στο νερό, οι δυνάμεις βάρους και άντωσης είναι ίσες, διότι βάρος = εκτόπισμα = άντωση. Το κέντρο βάρους G (σχ. 8) είναι το σημείο, που θεωρητικά βρίσκεται συγκεντρωμένα όλο το βάρος του σκάφους.
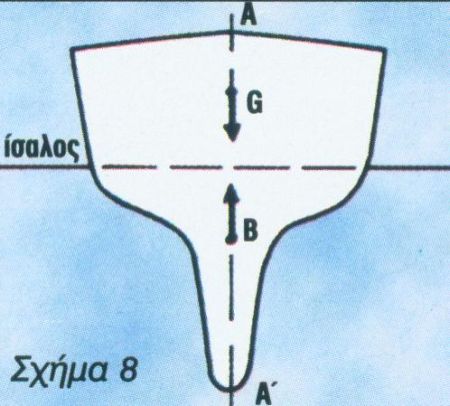
Αντίστοιχα, το κέντρο άντωσης είναι το σημείο, όπου συγκεντρώνονται όλες οι δυνάμεις άντωσης. Το κέντρο άντωσης συμπίπτει και με το γεωμετρικά κέντρο του όγκου των υφάλων του σκάφους (γάστρα). Οι διευθύνσεις των δυνάμεων βάρους και άντωσης εξασκούνται στα ομώνυμο κέντρα G και Β και είναι αντίθετες. Το μεν βάρος έχει διεύθυνση από πάνω προς τα κάτω, ενώ αντίθετα η άντωση, από κάτω προς τα πάνω. Επομένως, οι δύο αυτές δυνάμεις είναι ίσες και αντίρροπες. Λέμε, λοιπόν, ότι για να πλέει ένα σκάφος σε οριζόντια θέση, οι δύο δυνάμεις ενεργούν στο ίδιο επίπεδο, όπως φαίνεται στο σχήμα 8. Ας παρακολουθήσουμε όμως τι συμβαίνει, όταν το σκάφος πάρει κάποια κλίση με γωνία φ, στο σχήμα 9.
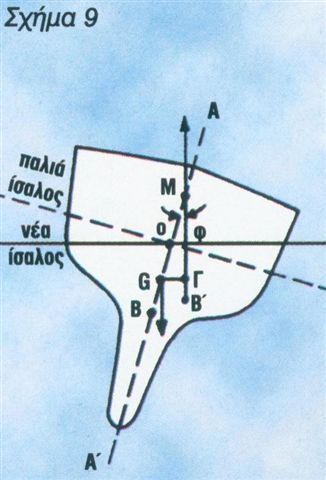
1. Το βάρος δεν μεταβάλλεται, ούτε ως προς το μέγεθος, ούτε ως προς τη διεύθυνση, ούτε ως προς το σημείο εφαρμογής του.
2. Η άντωση δεν μεταβάλλεται ως προς το μέγεθος, εφόσον βάρος = άντωση, ούτε ως προς τη διεύθυνση (από κάτω προς τα πάνω και κάθετη στην ίσαλο) το κέντρο όμως της εφαρμογής της μετατοπίστηκε στη θέση Β?, προς την πλευρά της κλίσης. Η μετατόπιση αυτή είναι βέβαια φυσικό επακόλουθο αφού, όπως είπαμε, συμπίπτει με το γεωμετρικό κέντρο της γάστρας, η οποία με την κλίση έχει αλλάξει σχήμα.
3. Στην κλίση αυτή με γωνία φ, οι δύο δυνάμεις εξακολουθούν να είναι ίσες και αντίρροπες, αλλά δεν ενεργούν στο ίδιο επίπεδο, άρα σχηματίζουν ένα ζεύγος
δυνάμεων, το λεγόμενο ζεύγος ευστάθειας, που τείνει να επαναφέρει το σκάφος σε οριζόντια θέση.
Μπορούμε, λοιπόν, να πούμε πως η ροπή του ζεύγους των δυνάμεων είναι ίση με το βάρος επί την απόσταση μεταξύ τους, δηλαδή η ροπή ευστάθειας είναι ίση με το εκτόπισμα D επί το μοχλοβραχίονα ευστάθειας GΓ. Αν τώρα προεκτείνουμε την ευθεία, που παριστάνει τη διεύθυνση της άντωσης προς τα πάνω, παρατηρούμε ότι θα τμήσει το μέσο άξονα του σκάφους ΑΑ? στο σημείο Μ, που λέγεται μετάκεντρο του σκάφους. Η απόσταση, τώρα, του μετάκεντρου Μ από το κέντρο βάρους G, δηλαδή η ευθεία MG λέγεται μετακεντρικό ύψος. Άρα μπορούμε να πούμε ότι από το ορθογώνιο τρίγωνο GΓΜ προκύπτει η απλή τριγωνομετρική σχέση GΓ = GM x ημ φ που, αν τη μεταφράσουμε, μας λέει πως ο μοχλοβραχίονας ευστάθειας GΓ είναι ίσος με
το μετακεντρικό ύψος GΜ επί το ημίτονο της γωνίας φ. Για δεδομένη, λοιπόν, γωνία (δηλαδή μία σταθερή τιμή ημ φ), ο μοχλοβραχίονας ευστάθειας, άρα και η ευστάθεια, εξαρτώνται από το μετακεντρικό ύψος MG.
Για να μπορέσουμε να υπολογίσουμε την ευστάθεια του σκάφους μας είναι απαραίτητο να προσδιορίσουμε πρώτα το μετακεντρικό ύψος MG κάτω από διάφορες γωνίες κλίσεις. Γι? αυτό καταφεύγουμε στο πείραμα ευσταθείας, που θα δούμε παρακάτω.
Δείκτες ευστάθειας και ιστιοφορίας
Θα γυρίσουμε για λίγο στο ιστιοφόρο σκάφος για να δούμε δύο πολύ ενδιαφέροντες δείκτες, που μπορούμε να υπολογίσουμε, έχοντας μετρήσεις όπως την απόσταση μεταξύ των κέντρων ιστιοφορίας (CΕ) και πλευρικής αντίστασης (CLR), καθώς και του μετακεντρικού ύψους ΜG.
(D = το εκτόπισμα σε κιλά, ΜG = το μετακεντρικό ύψος σε μέτρα, SA = το εμβαδόν ιστιοφορίας σε τετραγωνικά μέτρα και Η = η απόσταση του κέντρου
ιστιοφορίας CΕ από το κέντρο πλευρικής αντίστασης CLR).
Δείκτης ευστάθειας (ν):
ν = 0,046 x D x MG / SA x H
Είναι μία σχέση πολύτιμη για ένα ιστιοφόρο, γιατί αν πολλαπλασιάσουμε το δείκτη επί τη γωνία κλίσης του σκάφους, μπορούμε να προσδιορίσουμε κατά προσέγγιση τη δύναμη του αέρα, που απαιτείται για να δώσει μία ορισμένη κλίση στο σκάφος με το συγκεκριμένο εμβαδόν ιστιοφορίας. Με άλλα λόγια, μας λέει πότε πρέπει να πάρουμε μούδες και πόσες, για να ταξιδέψουμε με ασφάλεια και ταχύτητα.
Δείκτης ισποφορίας (f):
f = SA x H / 0,046 x D x MG
Είναι άλλη μία χρήσιμη σχέση, γιατί αν πολλαπλασιάσουμε το δείκτη επί την ταχύτητα του αέρα σε κόμβους, μπορούμε να προσδιορίσουμε τη γωνία κλίσης, δηλαδή το κουπαστάρισμα του σκάφους με τη συγκεκριμένη δύναμη του αέρα.
Οι παραπάνω δείκτες προσφέρουν δύο άριστους εμπειρικούς, αλλά και με μεγάλη προσέγγιση, τρόπους για να υπολογίσουμε την εγκάρσια ευστάθεια του σκάφους μας, σε σύγκριση με άλλα σκάφη του ιδίου μεγέθους. Ο πρώτος είναι να μετρήσουμε τη δύναμη του αέρα, που απαιτείται για να δώσει μία κλίση πλεύσης 20 μοιρών, έτσι ώστε να ταξιδέψουμε χωρίς πολλές τριβές και αντιστάσεις, εκμεταλλευόμενοι τις δυνατότητες του σκάφους μας σε ταχύτητα. Ας μην ξεχνάμε πως τα ιστιοφόρα είναι σχεδιασμένα έτσι, που όταν κουπαστάρουν γύρω στις 20 μοίρες δεν αλλάζει πολύ το σχήμα των υφάλων, άρα δεν δημιουργούνται επιπλέον τριβές. Ο δεύτερος είναι να διατηρήσουμε σταθερή τη δύναμη του αέρα και να μετρήσουμε τη γωνία κλίσης του σκάφους, για τον προσδιορισμό της ιστιοφορίας του.
Ευστάθεια μεγάλων κλίσεων και καμπύλη ευστάθειας
Είδαμε και αναλύσαμε πιο πάνω τα κέντρα άντωσης Β και βάρους G. Ας
συνεχίσουμε εδώ με άλλα στοιχεία, που προσδιορίζουν την εγκάρσια ευστάθεια ενός ιστιοφόρου σκάφους, που όπως είπαμε, είναι το πιο χαρακτηριστικό παράδειγμα στην ανάλυση της έννοιας της ευστάθειας.
Στο σχήμα 10 έχουμε το παράδειγμα ενός σκάφους, που παίρνει μία κλίση υπό γωνία φ. Η οριζόντια απόσταση του κέντρου βάρους G από το σημείο εφαρμογής της άντωσης Β? είναι η ευθεία GΖ, που είναι ο μοχλοβραχίονας ευστάθειας επαναφοράς (ροπή ευστάθειας = εκτόπισμα D x GΖ). Οι τιμές του GΖ υπολογίζονται για διαφορετικές γωνίες κλίσης, έτσι ώστε να γνωρίζουμε τα ελάχιστα όρια ευστάθειας μεγάλων κλίσεων και να μπορούμε να τα αποδώσουμε με την καμπύλη ευστάθειας.
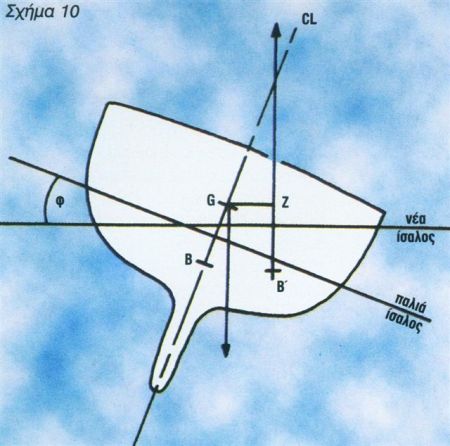
Η ευστάθεια ενός σκάφους έχει δύο παραμέτρους, ο συνδυασμός των οποίων επηρεάζει την εγκάρσια ευστάθειά Του. Η πρώτη παράμετρος είναι η ευστάθεια σχήματος (form stability) και η δεύτερη η ευστάθεια βάρους ή έρματος (ballast stability) όπως φαίνεται στο σχήμα 11. Στην πρώτη κατηγορία ανήκει το σκάφος α, που η ευστάθειά του εξαρτάται κυρίως από το σχήμα του κύτους του (φαρδύ και ρηχό σκαρί, με μεγαλύτερες αντιστάσεις στις κλίσεις).
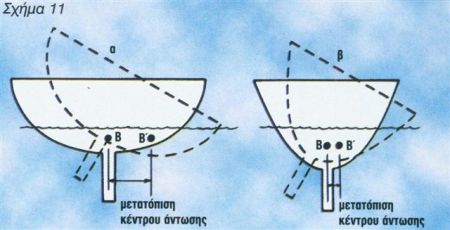
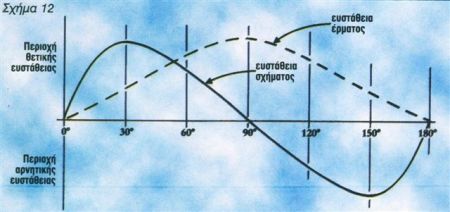
Αντίθετα, η ευστάθεια του σκάφους β εξαρτάται περισσότερο από το έρμα του (στενό σκαρί, με μεγάλο βύθισμα και έρμα). Στο σκάφος α, το κέντρο άντωσης μετατοπίζεται σε μεγαλύτερη απόσταση από το κέντρο βάρους, προς την πλευρά της κλίσης, σε αντίθεση με τα σκάφος β, στο οποίο η μετατόπιση είναι ελάχιστη. Το ιδανικό βέβαια είναι ένας συνδυασμός των δύο παραμέτρων. Στο σχήμα 12 μπορούμε να δούμε τα χαρακτηριστικά δύο καμπυλών ευστάθειας, η πρώτη βασισμένη στο σχήμα και η δεύτερη στο έρμα.
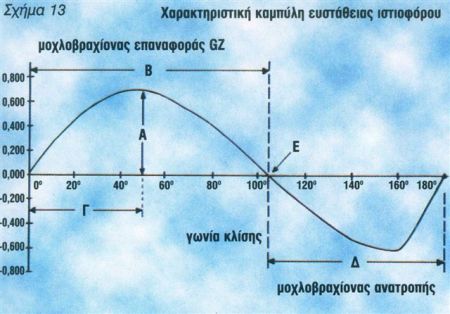
Αλλά για να εξοικειωθούμε περισσότερο με το «διάβασμα» μιας καμπύλης ευστάθειας, ας παρακολουθήσουμε το παράδειγμα του σχήματος 13, που ανήκει σε ένα σύγχρονο 14μετρο ιστιοφόρο. Τα πέντε κύρια σημεία, που μας λέει η καμπύλη είναι τα παρακάτω:
Α. Μεγίστη τιμή του μοχλοβραχίονα επαναφοράς GΖ, που στην προκειμένη περίπτωση είναι 0,686 μέτρα.
Β. Περιοχή θετικής εγκάρσιας ευστάθειας.
Γ. Η γωνία κατά την οποία ο μοχλοβραχίονας επαναφοράς GΖ αποκτά τη μέγιστη τιμή του, που στην προκειμένη περίπτωση είναι 50 μοίρες.
Δ. Περιοχή αρνητικής εγκάρσιας ευστάθειας.
Ε. Η γωνία μηδενικής εγκάρσιας ευστάθειας, όπου ο μοχλοβραχίονας επαναφοράς GΖ αποκτά μηδενική τιμή.
Το ελάχιστο όριο εγκάρσιας ευστάθειας διαφέρει από σκάφος σε σκάφος και ιδίως μεταξύ σκαφών διαφορετικών κατηγοριών, με ευστάθεια σχήματος και βάρους. Στο σχήμα 14 έχουμε δύο καμπύλες σκαφών διαφορετικών κατηγοριών. Όπως μπορούμε να δούμε, το σκάφος Α έχει μεγαλύτερη ευστάθεια σε μικρές γωνίες κλίσης, ενώ αντίθετα, το σκάφος Β υστερεί.
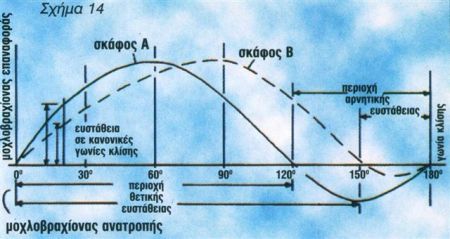
Σε μεγαλύτερες γωνίες κλίσης, τα σκάφος Β είναι σίγουρα πιο σταθερό και ανατρέπεται πολύ πιο δύσκολα από το σκάφος Α. Οι σχεδιαστές σκαφών βασίζονται πολύ στις καμπύλες ευστάθειας για μικρές σχετικά γωνίες κλίσης (25º-30º) μια και κάτω από τις γωνίες αυτές ταξιδεύουν συνήθως τα
ιστιοφόρα.
Πείραμα ευσταθείας
Όπως είδαμε παραπάνω, για να υπολογίσουμε την ευστάθεια χρειάζεται να προσδιορίσουμε πρώτα το μετακεντρικό ύψος MG. Σε γενικές γραμμές το πείραμα ευσταθείας γίνεται μεταφέροντας κάποιο γνωστό βάρος Β κατά μία γνωστή απόσταση L από τον κεντρικό άξονα του σκάφους, μετρώντας στη συνέχεια τη γωνία κλίσης (σχ. 15).
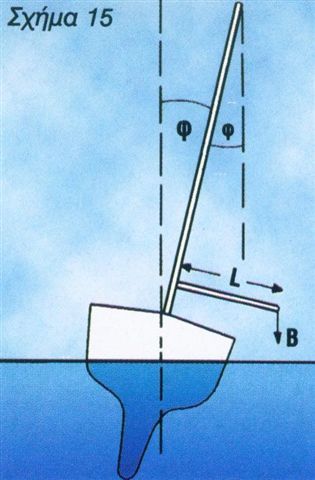
Με δεδομένο ότι ξέρουμε το εκτόπισμα του σκάφους μας, μπορούμε εύκολα να βρούμε τριγωνομετρικά την απόσταση του μετάκεντρου Μ από το κέντρο βάρους G, δηλαδή το μετακεντρικό ύψος ΜG (σχ. 9), για μία μικρή γωνία κλίσης, με τον τύπο:
MG = B x L / D x εφ φ
όπου Β είναι το γνωστό βάρος, L η γνωστή απόσταση που μετατοπίζουμε το βάρος, D είναι το εκτόπισμα του σκάφους και φ είναι η γωνία κλίσης που παίρνει το σκάφος με τη μετατόπιση του γνωστού βάρους κατά μία γνωστή απόσταση.
Το πείραμα ευστάθειας γίνεται κάτω από ορισμένες προϋποθέσεις και καταστάσεις, που για τη δική μας περίπτωση δεν χρειάζεται να αναφέρουμε παρά μόνο τις βασικές:
1. Το σκάφος πρέπει να πλέει ελεύθερο, χωρίς να εμποδίζεται από κάβους και άγκυρα.
2. Διαλέγουμε μία ήσυχη μέρα, χωρίς κύμα, αέρα ή ρεύματα. Ένα ήσυχο πρωινό αρόδου είναι το ιδανικότερο. Μπορούμε να περάσουμε ευχάριστα την ώρα μας επιχειρώντας ένα πείραμα ευστάθειας, που σίγουρα θα είναι
διασκεδαστικό αλλά και διδακτικό για την οικογένεια.
3. Το σκάφος δεν πρέπει να έχει κάποια κλίση. Μετράμε με ένα νήμα της στάθμης αν πλέει οριζόντια και κάνουμε τις απαραίτητες διορθώσεις.
4. Κατά τη διάρκεια του πειράματος δεν μετακινούμεθα ασκόπως στο
κατάστρωμα. Παραμένουμε στη θέση μας για να ζυγίσουμε το σκάφος και να κάνουμε τη μέτρηση.
5. Επιχειρούμε τις μετρήσεις στο φαρδύτερο σημείο του σκάφους, περίπου στο μέσον του καταστρώματος.
6. Αν το σκάφος είναι ιστιοφόρο, βγάζουμε τη μάτσο έξω και κάθετα στην κεντρική γραμμή του. Στη συνέχεια, χρησιμοποιώντας το βοηθητικό βαρκάκι, κρεμιόμαστε από κάποιο σημείο της και μετράμε την απόσταση που κρεμιόμαστε καθώς και τη γωνία που παίρνει κλίση το σκάφος, με το νήμα της στάθμης. Είναι καλύτερα να μετρήσουμε στο τμήμα του καταρτιού, που βρίσκεται κάτω από το κατάστρωμα, στην καμπίνα. Μπορούμε ακόμα να κρεμάσουμε στη μάτσα το ίδιο το βαρκάκι, αν φυσικά γνωρίζουμε το βάρος του.
7. Αν το σκάφος είναι μηχανοκίνητο, μεταφέρουμε όλους τους επιβαίνοντες από τη μία μπάντα, αν είναι μικρό ή με τη βοήθεια κάποιου ξύλου, φτιάχνουμε κάτι σαν τη μάτσα του ιστιοφόρου. Όσο πιο μακριά κρεμαστούμε, τόσο λιγότερο βάρος χρειάζεται.
8. Για να μετρήσουμε τη γωνία χρησιμοποιούμε ένα υπερευαίσθητο κλινόμετρο ή χρησιμοποιούμε τη μέθοδο του σχήματος 16.

Πρακτική εφαρμογή του πειράματος ευσταθείας
Με το πείραμα ευστάθειας μπορούμε να βρούμε με αρκετά μεγάλη προσέγγιση τη μέγιστη τιμή του μοχλοβραχίονα επαναφοράς και τη γωνία κλίσης, που θα μας δείξει τις δυνατότητες του σκάφους μας να ταξιδέψει με ασφάλεια. Αν, για οποιοδήποτε λόγο ξεπεράσουμε τη γωνία αυτή, υπάρχει πάντα ο κίνδυνος της ανατροπής. Αρκεί μόνο ένα κύμα από την μπάντα, όταν έχουμε φτάσει στην οριακή γωνία κλίσης, για να μας αναποδογυρίσει το σκάφος, με όλες τις συνέπειες.
Στην περίπτωση του ιστιοφόρου, η γνώση των ορίων μας είναι περισσότερο απαραίτητη, γιατί ταξιδεύουμε πάντα με κάποια κλίση. Στο μηχανοκίνητο σκάφος τα πράγματα είναι πιο απλά, αφού συνήθως ταξιδεύει στην οριζόντια θέση. Το κύμα όμως, σε συνδυασμό με τον αέρα, αλλά και τη συγκεκριμένη πλεύση μας, ανάλογα με το φορτίο, που μεταφέρουμε (άτομα, καύσιμα κ.λπ.), μπορεί να μας φέρει σε οριακό σημείο. Σε κάθε περίπτωση, με ιστιοφόρο ή μηχανοκίνητο, καλό είναι να βρούμε τα όριά μας, δηλαδή τη μέγιστη τιμή του μοχλοβραχίονα επαναφοράς και τη γωνία κλίσης, κάνοντας μόνοι μας ένα πείραμα ευσταθείας, με μετρήσεις του μοχλοβραχίονα επαναφοράς υπό διάφορες γωνίες κλίσης. Ξεκινάμε από μία γωνία έστω 20 μοιρών, αυξάνοντας σταδιακά το βάρος ή την απόσταση. Όσο μεγαλώνει ο μοχλοβραχίονας επαναφοράς GΖ, τόσο μεγαλύτερη κλίση δίνουμε (με την αύξηση του βάρους ή της απόστασης εφαρμογής του βάρους). Όταν
παρατηρήσουμε κάποια μείωση του μοχλοβραχίονα επαναφοράς GΖ, σημαίνει πως έχουμε πλησιάσει και έχουμε ξεπεράσει το οριακό σημείο της γωνίας κλίσης. Με άλλα λόγια, όσο μεγαλώνει η ροπή ευστάθειας, τόσο αυξάνουμε την κλίση του σκάφους κατά το πείραμά μας. Όταν η ροπή ευστάθειας αρχίσει να μειώνεται, tότε σημαίνει πως έχουμε ξεπεράσει τη μέγιστη ασφαλή γωνία κλίσης. Οι σχέσεις, που διέπουν την πρακτική εφαρμογή του πειράματος ευσταθείας είναι:
GZ = MG x ημ φ
ημ φ / συν φ = εφ φ
ροπή ευστάθειας = εκτόπισμα D x GZ = D x MG x ημ φ
MG = B x L / D x εφ φ
(όπου Β είναι το γνωστό βάρος, L η γνωστή απόσταση που μετατοπίζουμε το βάρος, D είναι το εκτόπισμα του σκάφους και φ είναι η γωνία κλίσης που παίρνει το σκάφος με τη μετατόπιση του γνωστού βάρους κατά μία γνωστή απόσταση). Για την επίλυση της παραπάνω σχέσης, σας δίνουμε τις
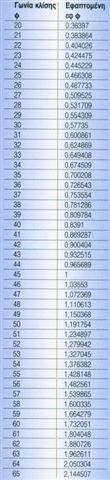
εφαπτόμενες των γωνιών κλίσης από 20 μοίρες, για να γίνει ο υπολογισμός σας πολύ πιο εύκολος, με απλά μαθηματικά, αν και στη μέτρηση της γωνίας με τo νήμα της στάθμης η εφαπτομένη της γωνίας κλίσης δίνεται από τον τύπο εφ φ = α/μ.
Όσο μεγαλώνει το ΜG, αυξάνουμε τη γωνία κλίσης. Όταν σταματήσει να
μεγαλώνει ή αρχίσει να μικραίνει, έχουμε φτάσει στη μέγιστη τιμή του
μοχλοβραχίονα επαναφοράς GZ, άρα και στη μέγιστη επιτρεπτή γωνία κλίσης φ, που κάνει το σκάφος ασταθές.